Porque 4 ⋅ 4 ⋅ 4⋅ = 64 4 ⋅ 4 ⋅ 4 ⋅ = 64, escribimos 43 = 64 4 3 = 64 y decimos, "4 cubos son 64". También usamos esta notación para unidades cuadradas y cúbicas. Un cuadrado con longitud lateral de 5 pulgadas tiene área 25 en 2. Un cubo con borde largo 4 cm tiene volumen 64 cm 3. Para leer 25 en 2, decimos "25 pulgadas.. Calculadora gratuita de números complejos - Simplificar expresiones complejas utilizando reglas algebraicas paso por paso. Número de línea. Relacionado. Ejemplos. i^3 ; i^{22} (3+2i)(3-2i) \frac{1}{1+2i} Mostrar mas; Descripción. Simplificar expresiones complejas utilizando reglas algebraicas paso por paso.. Por favor añade un.

EULOLO CUADRADO Y CUBO DE UN NÚMERO NATURAL

Cubo y cuadrado de un número Ficha interactiva

CUADRADO Y CUBO DE UN BINOMIO

Quinto primaria. Matemáticas.Cuadrados y cubos perfectos YouTube

El cuadrado y el cubo de un número
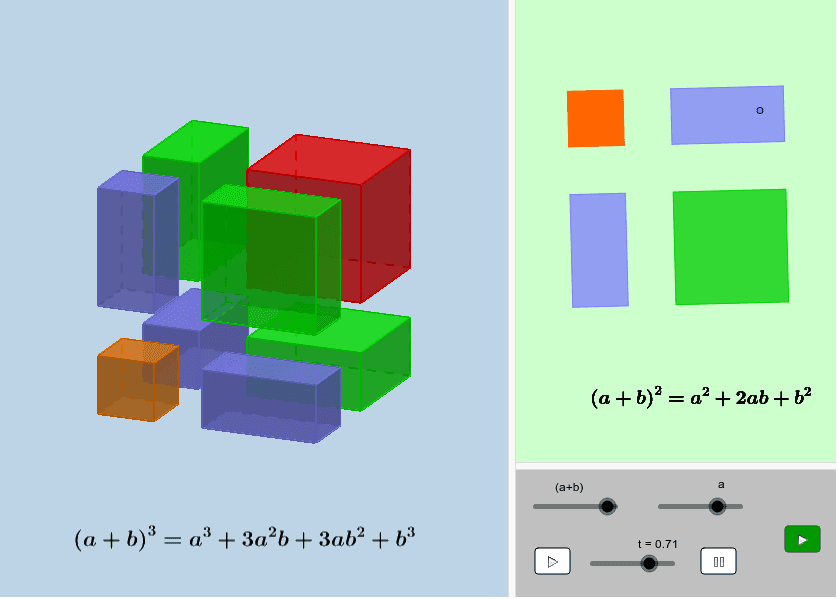
Cuadrado y cubo de un binomio GeoGebra

Cuadrado de un numero complejo YouTube

Números complejos cuadrado de un binomio YouTube

4TO AÑO CUADRADO Y CUBO DE UN BINOMIO EJEMPLOS YouTube

Potencia de unidad imaginaria. Cuadrado y Cubo de un complejo YouTube

Números ComplejosParte real e imaginariaOpuesto y Conjugado YouTube

¿APRENDEMOS JUNTS? LAS POTENCIAS AL CUADRADO Y AL CUBO.

POTENCIAS AL CUADRADO Y CUBO YouTube

CUADRADO de un NÚMERO COMPLEJO SUPER FÁCIL 🤩 YouTube
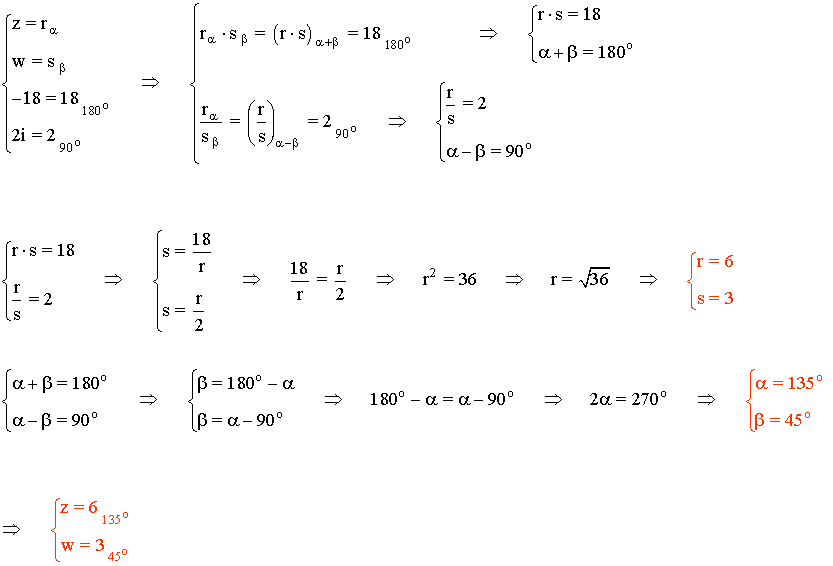
Ejemplos resueltos de problemas con números complejos. Ecuaciones con

18 Cuadrado y Cubo de Números Complejos YouTube

Clase digital 5. Productos notables Binomio al cuadrado, Binomio al

BINOMIO AL CUADRADO CON COMPLEJOS YouTube

Potenciación de números complejos usando cuadrado y cubo de un binomio

Módulo y argumento de un número complejo YouTube
Números complejos y factorización de sumas de cuadrados. Aprende cómo las expresiones de la forma x^2+y^2 pueden ser factorizadas en factores lineales. ¡Esto no sería sin la ayuda de los números complejos! Creado por Sal Khan.. (Si tomas la diagonal del cuadrado unitario y colocas un extremo en 0 , el otro extremo coresponde al número 2 ). Similarmente, todo número complejo de hecho existe, pues ¡corresponde a una ubicación exacta en el plano complejo! Quizá al poder visualizar estos números, podamos entender que llamar "imaginarios" a estos números fue.