En este vídeo se expone la demostración hecha por el matemático Ivan Niven (Véase el archivo de Wikipedia: https://goo.gl/VBPdEM) de forma detallada.Este víd.. Actualizado el 14 de Marzo del 2020 12:00 AM. Este 14 de marzo el número está de fiesta. Quién lo descubrió, cómo es, cómo se sabe que es irracional, y más te lo explicamos en esta nota.

Demostración de que raíz de 2 es irracional Aprendo en Línea ESTUDIANTE. Currículum Nacional

Demostracion de PI YouTube

¿Qué es Pi? YouTube

Número PI es la relación entre la longitud de una circunferencia y su diametro, en geometría

Día de Pi Todo lo que debes saber sobre 'π', el número irracional más famoso RPP Noticias

Demostración de que PI es irracional ¡El vídeo que tu profe de mates no quiere que veas! YouTube

El Enigma del Numero Pi 50 datos interesantes

Demostración de Pi GeoGebra

Demostración de que la suma de un racional con un irracional es irracional YouTube

Día de Pi Todo lo que debes saber sobre 'π', el número irracional más famoso RPP Noticias

Uma prova simples de que pi é irracional YouTube

Descubre el Significado del Símbolo Pi Historia, Matemáticas y Más Que Significan Los

π es irracional LA HISTORIA DE PI Universidad de Oriente Veracruz

O Número Irracional De Constante Matemática Do Símbolo Do Pi No Círculo, Letra Grega Ilustração

El número Pi
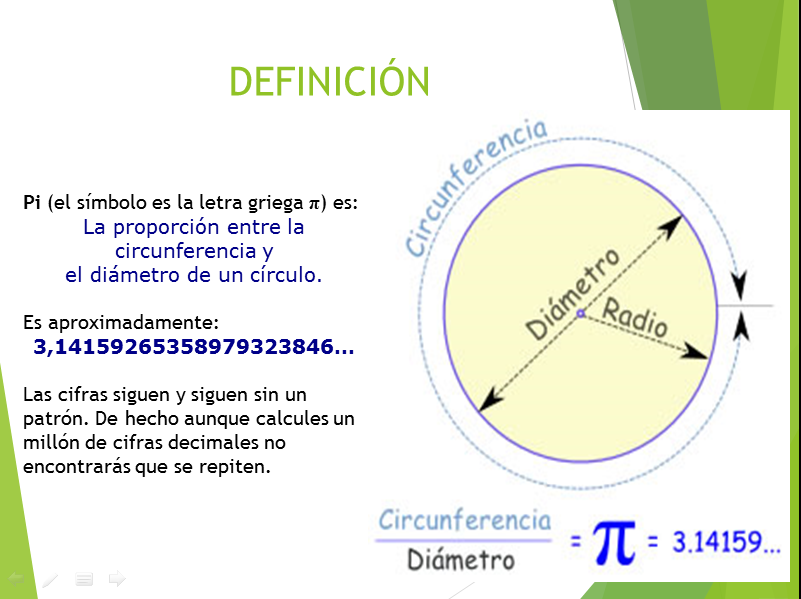
Números Irracionales.

ROL Science Divulgación científica Astronomía y mucho más NASA en español Los misterios

Raíz de 2 es irracional. YouTube
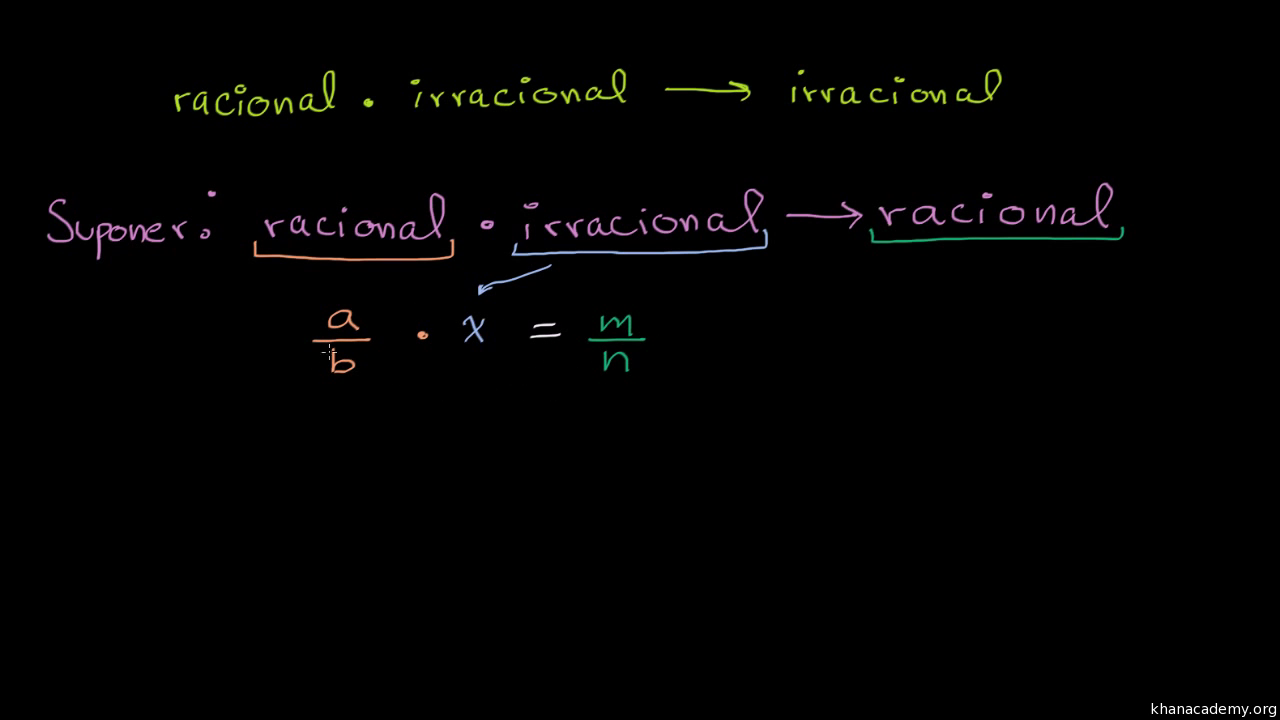
La Suma De Dos Numeros Irracionales Es Un Numero Irracional

El Fondo Del Número Irracional Del Constante Matemático Del Símbolo Del Pi Y De Muchas Fórmulas
Bueno, para esto que te parece si este racional, el del principio, le ponemos un nombre, a este de aquí lo voy a ver como "a" entre "b", ok. "a" entre "b" lo voy a multiplicar por un número irracional y como un número irracional es muy, pero muy, pero muy largo lo voy a denotar con "x", mi número irracional, este número irracional le voy a.. El número es trascendente. Vamos a demostrar el siguiente resultado: Teorema: El número es trascendente sobre . Demostración. En primer lugar tenemos que si fuera raíz de un polinomio con coeficientes en , entonces el número también sería raíz de un polinomio de este tipo (no necesariamente del mismo). Sea este polinomio .